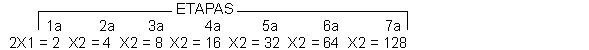|
RADIO INSTITUTO CURSO DE CIRCUITOS DIGITALES LECCIÓN Nº 8 CIRCUITOS
CONTADORES - TEMPORIZADORES LOS
INTEGRADOS CD4020, CD4040, CD4060 Y CD4541 - DIVISORES X 4, X8, Y POR UN
NÚMERO CUALQUIERA - BASE DE TIEMPOS - RELACIÓN DE FRECUENCIA Y TIEMPO - RELACIÓN
DE CICLO ACTIVO Y FRECUENCIA - TIMER PROGRAMABLE CON CD4541. Cuando
se trata de dividir una señal de frecuencia determinada, es necesario
recurrir a los oficios de un integrado contador que realice tal división. Si
la necesidad es de dividir por 2, la solución es muy sencilla ya que con un
simple flip-flop sabemos
que se produce tal división, si fuera por 4, la operación continúa siendo
sencilla porque simplemente se acopla la salida del primer flip-flop con la entrada
del segundo y como éste vuelve a dividir por 2, finalmente en la salida del
segundo se obtiene el resultado buscado. Para
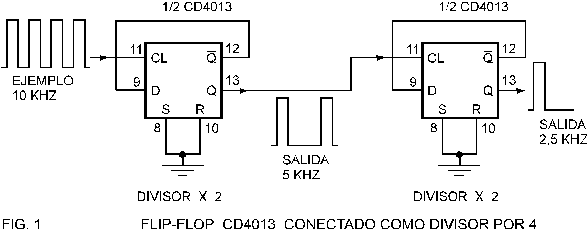
una operación de este tipo puede utilizarse un flip-flop CD4013, que ya hemos estudiado, y la forma de
conectarlos entre sí la vemos en la figura 1.
Si
se necesita continuar la división por cifras mayores, podríamos seguir
enlazando mas flip-flop de
este tipo, pero es indudable que esto significará un derroche en tiempo,
espacio, material y dinero totalmente innecesario dado que hay integrados
específicos para este fin. De
lo expuesto se deduce que un circuito integrado contador está compuesto por
una serie de flip-flops interconectados
entre sí a fin de lograr la división de un número cualquiera. Según
la cantidad de biestables que contengan
en su interior, será la cifra máxima de división que se obtenga. Cada Flip-flop es considerado
como una etapa, y así figura en los manuales, de modo que lo observado en el
esquema de la figura 1, bien podríamos considerarlo como un contador de 2
etapas. Cada etapa (flip-flop)
divide por 2; la siguiente vuelve a dividir por 2 el resultado de la anterior
y así sucesivamente con todas las etapas hasta llegar a la última. La
expresión binaria será en base a la potencia de 2 y de esta forma se obtiene
la cifra de división según la etapa en que se tome la salida definitiva que
necesitamos. Por
ejemplo, el "contador" implementado en la figura 1 es de 2 etapas,
por lo tanto la cifra de división que puede efectuar es la siguiente: Si se
toma la salida en la primer etapa, 21 = 2 , o sea que divide por 2, en la segunda, 22 = 4, es decir divide por 4. Hay
contadores de distinta cantidad de etapas, algunos disponen de salidas en
todas, en otros puede faltar una o mas, así es que tenemos el contador CD4024
que dispone de 7 etapas y todas tienen acceso. Veamos que factor de división
se obtiene en la salida de la etapa 5a: 25 = 32 y el máximo
posible será en la última o sea la 7a: 27 = 128. Para
quienes no estén muy prácticos en operaciones matemáticas de potenciación, le
diremos que tomen una calculadora que permita acceder a una constante. ponga el número 2 como constante y luego X 1 y
apriete la tecla =, el resultado será la división de la primer etapa, o sea
2; luego continúe apretando la tecla = para lograr el factor de las
siguientes etapas. Así apretando 7 veces la tecla = (igual) partiendo del
número 1, se obtiene el resultado del factor de división de la 7a etapa que
será 128. Si
la calculadora no permite acceder a una constante, comience por multiplicar
por 2 la primer etapa y continúe
multiplicando por 2 los resultados obtenidos tantas veces como etapas quiera
saber. Por
ejemplo, en este integrado, será así:
Estos
integrados, al igual que el CD4024, son todos contadores binarios y están
constituidos por una cadena de flip-flops que componen sus etapas. Debido a la
limitación que impone la cantidad de terminales de su encapsulado, no todos
tienen acceso a las salidas de todos los biestables,
por lo general cuantas mas etapas tienen más salidas quedarán aisladas, pero
en contrapartida se logran factores de división mas elevados. El
CD4020 es un contador binario de 14 etapas, tiene acceso a 12 de ellas y
falta en las etapas segunda y 3a; el máximo factor de división obtenible,
como ya hemos dicho está dado por la cantidad de etapas, por lo tanto es de 214 =
16.384. El
CD4040 es un contador de iguales características que el anterior pero de 12
etapas, por este motivo, al tener igual cantidad de patitas (16) es posible
obtener salidas en todas las etapas, pero la cantidad de divisiones que se
logran es bastante menor, en este caso es de 212 = 4096. Con
el CD4060 sucede algo similar al 4020, es decir que también poseemos 14
etapas con lo cual se alcanza el mismo número de divisiones, pero en este
caso no se tiene acceso a las etapas 1a, 2a, 3a, y 11a, pero ofrece la
posibilidad de armar un oscilador RC (resistencia-capacitor)
en los terminales 9, 10, y 11. Este oscilador se puede armar o no, según la
aplicación que se de al integrado, por ejemplo si se usa como temporizador,
conviene realizarlo porque de otro modo hay que armar otro externamente con
mas componentes y aplicar la señal a la entrada del pin 11. Para
efectuar una división con estos integrados lo primero que debe hacerse es
determinar que salidas se van ha utilizar, y luego elegir el que nos permite
realizarla, que muchas veces puede ser cualquiera de ellos. Sin embargo, y a
modo de ejemplo, puede suceder que haga falta dividir una señal determinada
por 2048, (211) que corresponde a la etapa 11a o mejor dicho
al biestable Nº 11 de una cadena.
Pues bien, en este caso no es posible usar el 4024 porque solo tiene 7. Tampoco
podemos usar el 4060 porque esta etapa no tiene acceso, en cambio puede
utilizarse un 4020 o un 4040, ya que ambos superan la etapa 11a y disponen de
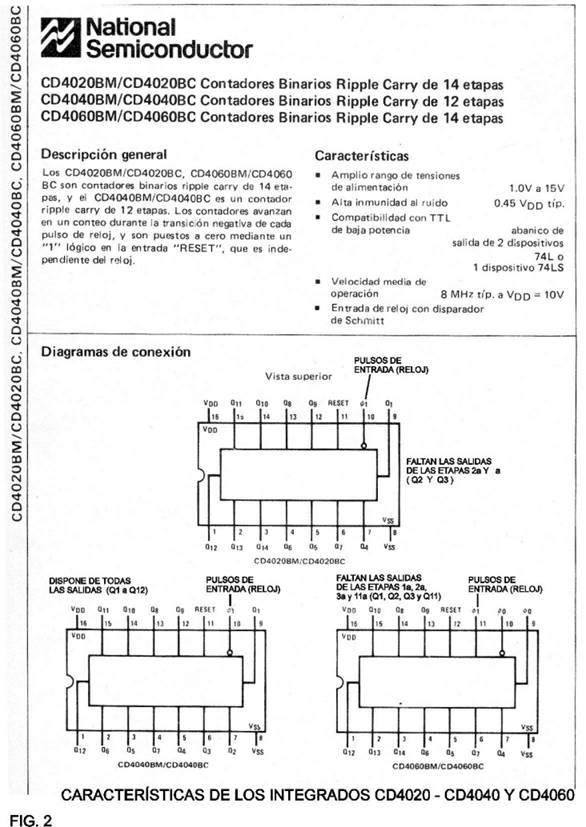
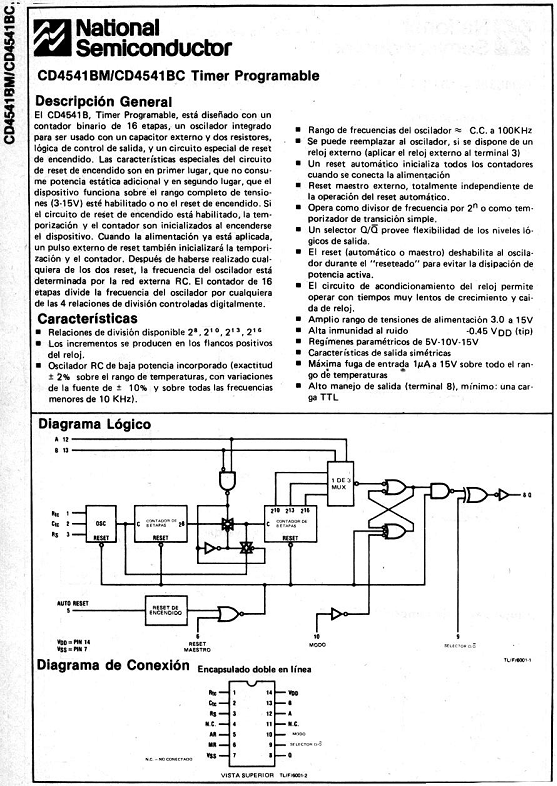
esta salida. En
la figura 2 exponemos la información de estos integrados extraída del
manual National.
Hasta
aquí hablamos de las divisiones que se obtienen en cada etapa y la cantidad
máxima que ofrece cada integrado de acuerdo a los biestables que
lo componen. Pero
en realidad, no son muchas las veces que se necesite una división por una
cifra coincidente con una sola de las salidas, sin embargo tampoco hay
problemas para realizarla, vamos a ver como se consigue la división por un
número cualquiera. Si
la cifra no supera la capacidad máxima del integrado, se usará uno solo, si
fuera mayor deberán implementarse dos o mas en cascada hasta lograr la cifra
buscada, del mismo modo que lo visto en la figura 1 con el 4013, es decir
conectando la salida del primero con la entrada del segundo y acondicionando
éste para la nueva división. Vamos
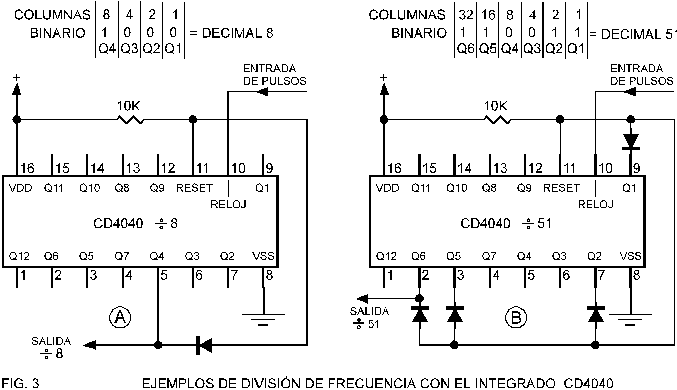
a clarificar este concepto con los siguientes ejemplos, usando para ello el
integrado CD4040, si bien sabemos que podría ser otro. Figura
En
la figura En
B, la división es por 51, y en este caso se utilizan 4 salidas para lograr
este factor, de todos modos, aunque lleve mas elaboración sigue siendo
sencilla. Ahora
veamos porque el integrado logra dividir por cualquier cifra: Observe
que el terminal de reset está conectado a
positivo (1), mediante una resistencia de 10K, y a su vez, en este
mismo terminal se conectan los ánodos de
los diodos que forman el factor de división. Los cátodos de todos los diodos
que se empleen, siempre se conectan a las salidas Q que correspondan. Antes
de iniciar la cuenta, todas las salidas Q se encuentran a potencial de masa,
es decir 0, por lo tanto el reset también está a 0, porque los diodos en
cuestión quedan en directa para este terminal y
drenan la corriente que circula por la resistencia de 10K hacia las salidas. Con
un 0 en reset el contador está habilitado para efectuar la cuenta, la que
efectivamente se produce en cada flanco de bajada, o transición negativa, de
los pulsos de entrada. Continuamos
la explicación con lo que sucede en A de la figura 3: El primer pulso de
conteo, produce el cambio de estado de En
este momento aparece por un instante un pulso de salida de nivel alto.
Decimos por un instante porque al cambiar a 1, el diodo conectado con el
reset ya no "roba" la tensión que existía, porque pasa a tener el
mismo potencial en ambos extremos (positivo en ánodo y cátodo), y de esta
manera no conduce y aparece un 1 con el nivel positivo de fuente a través de Ahora
bien, una vez producido el reset, todas las salidas retornan a 0, también Q4,
con lo que nuevamente la entrada reset pasa a 0 porque el diodo nuevamente
drena la tensión de éste terminal hacia De
acuerdo a este análisis, se observa que cada 8 pulsos en la entrada, el
contador dará un pulso de salida en Q4, cumpliéndose la división por 8. Preste
atención a la secuencia de unos que van apareciendo en las salidas, y se dará
cuenta que siguen el ritmo de conteo, y van adoptando una notación binaria
que indica en todo momento la cantidad de pulsos que está contando. Ejemplo:
contó 3 pulsos = Q1 y Q2 en estado alto (3 en binario). En Efectivamente,
en ese momento las salidas Q6, Q5, Q2 y Q1 estarán en 1, que corresponde en
binario al decimal 51, y de esta manera ninguno de los 4 diodos estará
drenando a masa la tensión de reset, por lo que también dicha entrada pasa a
1 y lleva a 0 todas las salidas, reiniciándose un nuevo ciclo del mismo modo
que en el caso anterior. En
el diseño de una etapa contadora, conviene primero dibujar una escala de
columnas del sistema binario a fin de hallar fácilmente el número que le
corresponde a la cifra decimal por la que queremos efectuar la división y
debajo anotar las salidas Q del integrado que corresponden a cada dígito
binario. Ya sabemos que el Q1 corresponde al dígito menos significativo, o lo
que es lo mismo, a la columna de menor valor, que es la de la derecha, y la
salida del divisor se toma de la última etapa de la izquierda que tenga un 1,
y que corresponde al dígito mas significativo. Luego
vemos en las columnas cuales son las que tienen un 1 y a que salida Q
corresponden, y simplemente se conectan diodos en todas (las que tienen un
1), siempre el cátodo hacia la salida y el ánodo hacia la
entrada reset, dejando sin conexión las que no se utilizan, que son las que tienen
0. Hemos
incluido una tabla de éste tipo a modo de ejemplo en los esquemas A y B. BASE
DE TIEMPOS DE 50 HZ En
ocasiones es necesario disponer de una base de tiempos precisa de una
frecuencia determinada, y si bien hay varias maneras de lograrlo, lo mas conveniente es realizar un oscilador de alta
frecuencia y luego dividir por un factor que entregue finalmente la
frecuencia que necesitamos. Incluso
si los requerimientos son de alta precisión, es necesario el uso de un
cristal en el oscilador que asegure una frecuencia exacta y sin corrimientos. Vamos
a suponer que necesitamos una base de tiempos de 50 Hz para
controlar un aparato determinado. Lo
mas sencillo de realizar es un oscilador astable de
50 Hz dotado de un preset que nos permita ajustar la frecuencia y ya
está, podemos dar por resuelto el problema. Pero
en realidad no es tan así: Si con esta señal se gobierna un temporizador que
establece un tiempo de acción de algún electrodoméstico,tal vez
no haya problemas si sufre algún corrimiento entre 48
y 52 Hz, que significa un error de un 5%
aproximadamente en mas o en menos. Esto
traerá como consecuencia que si dicho temporizador se programa para un tiempo
de acción de una hora, o sea 60 minutos, puede llegar a funcionar en algunas
ocasiones 57 minutos, y en otras 63
minutos. Normalmente
esta situación no acarrea inconvenientes, pero que pasa si los 50 Hz son utilizados como base de tiempo de un
reloj horario ?, indudablemente este error
puede llegar en el término de 24 horas a diferencias tan notables como una
hora y 12 minutos de más o de menos que la realidad. Con
esta explicación queremos significar la importancia que puede tener una
variación de pocos Hz cuando se trata de
una frecuencia que ha sido tomada como base de tiempos de acción de distintas
maquinarias o artefactos y la precaución que debe tomarse de acuerdo a la
exigencia operativa del aparato. De ahí la importancia de realizar
osciladores de alta frecuencia aunque la necesidad sea de una señal de baja
frecuencia, la exactitud que se consigue es infinitamente superior, porque
variaciones de pocos Hz se van perdiendo
en las sucesivas divisiones y prácticamente no afectan el resultado final,
por lo tanto se logra una estabilidad muy grande en la salida. Por
ejemplo, si la señal de 200.000 Hz que se
aplica en la entrada del integrado de la figura 4 sufre un desplazamiento de
10 Hz en mas o en menos, el resultado
final de la división no se verá afectado porque prácticamente no causa
efectos; vamos a comprobarlo: 200.010 / 4000 = 50,0025 Hz. Estos
decimales, que corresponden a las milésimas de Hz,
no causarán ningún problema. En
el caso anterior, 2 Hz de corrimiento,
producían serios inconvenientes y en cambio con el uso de alta frecuencia y
luego el divisor, 10 Hz o mas de
desplazamiento no acarrean dificultades. En
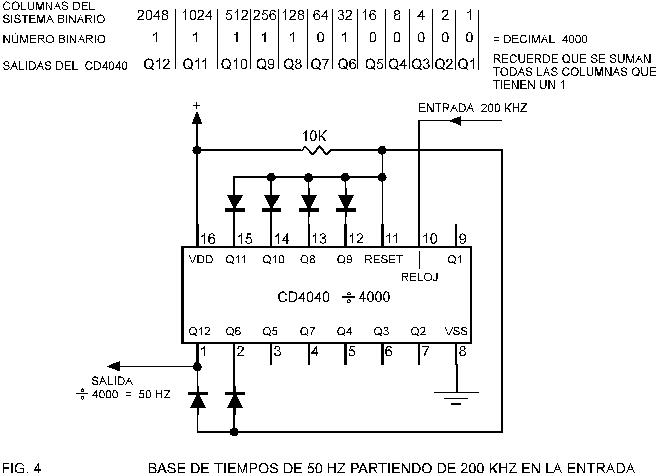
la figura 4 representamos este contador divisor por 4000 que entrega salida
de 50 Hz.
Este
circuito, al igual que los anteriores no ofrece mayores dificultades de
montaje, solamente hay que conectar 6 diodos en las salidas Q indicadas en la
tabla de arriba y que corresponden a las columnas que tienen un 1. En
todos los casos que se nos presenten donde sea necesario realizar un contador
divisor por una cifra determinada, se debe proceder como sigue: Para ello
vamos a tomar como ejemplo el esquema de la figura 4. Partimos
del oscilador, que en este caso lo hemos determinado en 200 Khz (200.000 Hz). Luego
buscamos el factor de división para lograr los 50 Hz,
dividiendo 200.000 / 50, esto nos da un resultado de 4000, este resultado es
el factor de división. 200.000 / 4000 = 50 Digamos
que la frecuencia del oscilador puede ser cualquier otra, aunque siempre
conviene que los resultados arrojen números enteros. Por ejemplo, si la
frecuencia del oscilador fuera de 27000 Hz, el
factor de división para conseguir salida de 50 Hz será:
27000 / 50 = 540, o sea que hay que preparar el integrado para que divida por
540. Bien,
sigamos con Comprobamos
sumando el valor de cada columna que tiene un 1 que no hay error; debe dar en
decimal 4000. Verificamos
que el integrado tiene la cantidad suficiente de etapas que permitan esta
división, el CD4040 tiene 12 y ya sabemos que permite un máximo de 212 =
4096, por lo tanto en este sentido es apto. Luego
anotamos en el gráfico que hemos confeccionado las salidas Q del integrado
que correspondan a las columnas binarias. Verificamos
que el integrado dispone de salidas Q en todas las columnas que tienen un 1, el
4040 las tiene todas. Vea que en este caso el 4060, que tiene 14 etapas y
permite factores de división mucho mayores,
no resulta útil porque falta el acceso en la salida 11a, y en este caso es
necesaria. Podría
obviarse alguno de estos pasos, pero nos parece que de este modo se trabaja
con mayor seguridad y es mas difícil
cometer errores. Una
vez comprobado que no hay errores, se procederá a conectar el integrado y sus
componentes asociados. El
funcionamiento es igual que en los casos anteriores, o sea que cuando la
división llega a 4000, las salidas del integrado adoptarán los estados altos
y bajos correspondientes a este número en binario, que es coincidente a lo
que habíamos anotado previamente en las columnas. De este modo todas las
salidas en las que se han dispuesto los diodos estarán en 1, por lo tanto en
el Q12 aparece el pulso y se produce el reset dando lugar a la iniciación de
un nuevo ciclo de divisiones. TIMER
PROGRAMABLE CON EL INTEGRADO CD4541 Por
lo general todas las publicaciones de electrónica presentan temporizadores y
distintos Timers basados en un integrado
muy conocido: el 555. Este
integrado tiene un sinnúmero de aplicaciones posibles, generalmente
relacionadas con el control de tiempos y otras variables referidas a la
conformación del ancho de los pulsos de salida, tal es así que en plaza y en
distintos artículos escritos se lo conoce como "el temporizador
555"; oportunamente lo trataremos en profundidad en este curso. Pero
sucede que existe un circuito integrado poco conocido con el que se pueden
realizar Timers y temporizadores muy
versátiles, superiores en las prestaciones finales a las que podrían
obtenerse empleando el 555, concretamente estamos hablando del CD4541. Con
este integrado se pueden realizar sencillos y precisos temporizadores
programables en intervalos de segundos, minutos, horas y hasta días.
Las
aplicaciones o usos que se pueden presentar son muy variadas, podemos citar
algunos casos a modo de ejemplo. Mantener
encendido durante un tiempo preestablecido cualquier aparato eléctrico, como
ser un ventilador, acondicionador de aire, el televisor, una lámpara, la iluminación
de una vidriera etc. etc., solo será necesario programarlo con el tiempo de
acción que se desee para mantener activado el artefacto conectado a Como
podemos ver, de acuerdo a la descripción general del manual, el circuito está
diseñado con un contador binario de 16 etapas y un oscilador integrado para
ser usado con dos resistencias y un capacitor externos.
Este contador es igual al CD4060 que hemos estudiado, solo que tiene dos
etapas mas (16 en total) por lo que se consigue un factor de división mayor,
216 = 65536. De
hecho si quisiéramos podríamos realizar un temporizador de iguales
características con el CD4060, pero no lograríamos este factor de división
porque solo dispone de 14 etapas, por otra parte para lograr las prestaciones
y versatilidad del que exponemos, hacen falta otros componentes externos que
complican el diseño. Naturalmente nada de esto se justifica siendo que
disponemos de un integrado que simplifica todo el desarrollo y se logra un
producto de excelentes características con pocos componentes. RELACIÓN
DE FRECUENCIA Y TIEMPO A
continuación vamos a explicar la relación que existe entre la frecuencia del
oscilador y el tiempo de acción del temporizador. La
frecuencia que se determine en el oscilador siempre está referida a Hertz (ciclos
ó pulsos) por segundo, o sea que si se establecen 100 Hz, significa que en un segundo el oscilador genera 100
pulsos de onda cuadrada. Así también podemos hablar de frecuencias mucho menores, por ejemplo 1 Hz quiere
decir que se forma un pulso por segundo; 0,5 Hz significa
que en un segundo se habrá formado medio ciclo, por lo tanto en este caso la
formación completa del pulso tarda dos segundos. En
la figura 6 se aclaran estos conceptos.
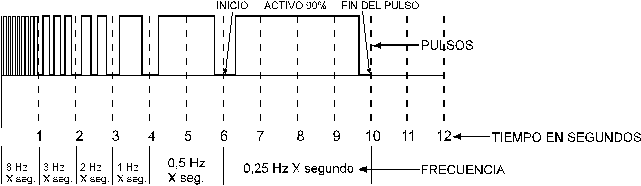
Como
vemos en la figura 6, la primer columna tiene 8 pulsos que ocupan 1 segundo
de la escala de tiempo, por lo que diremos que corresponde a una frecuencia
de 8 Hz; la segunda tiene 3 pulsos en un
segundo, por lo que la frecuencia será de 3 Hz;
y así llegamos a la última que tiene un pulso que ocupa 4 segundos en
formarse, por lo tanto la frecuencia, que siempre se relaciona con un
segundo, será de 1 dividido 4 = 0,25 Hz.
El ciclo completo se considera desde su inicio en la formación a la izquierda
de la base, y termina en el final a la derecha de la base. Esto
significa que a los fines de determinar la frecuencia, no es importante el
ancho del pulso sino el período de tiempo que ocupa desde su inicio hasta el
fin, o sea el ciclo completo. El
ancho determina el tiempo que está activo dicho pulso y que se expresa en porcentaje
del ciclo total, en el caso de este ejemplo corresponde al 90%, es decir que
considerando desde el inicio hasta el fin, se encuentra en estado alto el 90%
del tiempo y el 10% en estado bajo. En la figura 7 ilustramos otros
porcentajes de actividad que aclaran lo dicho.
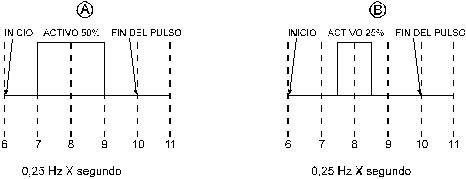
En
A de la figura 7 vemos un pulso con actividad del 50% del ciclo total, dado que
sobre 4 segundos de duración del ciclo completo, se mantiene en estado alto
por 2 segundos. En
B la actividad es del 25% porque el estado alto se sostiene durante 1 segundo
y el estado bajo por lo tanto es de 3 segundos. En
los tres casos expuestos los pulsos tienen anchos distintos que determinan el
tiempo de actividad, pero la duración o período del ciclo completo es igual
en los tres, o sea de 4 segundos, por ende la frecuencia no se modifica y por
lo tanto continúa siendo de 0,25 Hz. El
tema del ancho de pulso o porcentaje de actividad es de suma importancia en
determinadas circunstancias, por eso nos pareció importante tratarlo en esta
lección, aunque en el caso del temporizador que nos ocupa no tiene relevancia. Efectivamente,
como en este circuito se usa un contador binario como base de tiempos
(incluido en el integrado CD4541) , lo único
que nos interesa es la frecuencia de reloj, independientemente del ancho que
se conformen los pulsos. Los
tiempos que se obtienen en las distintas salidas de un contador binario
tienen relación directa con la frecuencia de reloj y la base de un
segundo que yá hemos dicho. De
este modo cada división que se produce introduce una demora proporcional a la
frecuencia. Suponiendo
una frecuencia en el oscilador de 1 Hz (sabemos
que es un ciclo o pulso por segundo) y tomamos la salida en el Q4, que
corresponde a un factor de división por 8, la demora será de 8 segundos
dividido por 2, o sea = 4 segundos. Si
en cambio la salida se toma en el Q16 que corresponde a un factor de división
de 65536, la demora será de 65536 segundos dividido por 2 = 32768 segundos. Estas
cuentas son muy fáciles de realizar porque la frecuencia de 1 Hz es igual a 1 segundo, con frecuencias mayores o
menores los resultados no serán "redondos". Este
integrado (4541) solo permite que la salida tenga acceso a las etapas 8, 10,
13 y 16, y se logra mediante la combinación de estados altos y/o bajos en los
terminales 12 y 13. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
E-mail: radioinstituto@gmail.com - Sitio web: www.radioinstituto.com.ar |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||