|
RADIO INSTITUTO
CURSO DE
ELECTRÓNICA – 2
LECCIÓN
Nº 3
RELACIONES ENTRE I, V y
R – LEY DE OHM – APLICACIONES DE LA LEY DE OHM –
ÓHMETROS Y VOLTÍMETROS – SENSIBILIDAD DE LOS
VOLTÍMETROS – PRECISIÓN Y EXACTITUD – LEYES DE
KIRCHHOFF – PUNTOS EQUIPOTENCIALES – CAJAS DE RESISTENCIAS
– OTRAS FORMAS DE PUENTE DE WEATSTONE – CIRCUITOS DELTA Y
ESTRELLA – SHUNTS – MILIAMPERÍMETROS.
RELACIONES ENTRE I, V, y R
Las características
fundamentales de la corriente que circula por un circuito eléctrico
cerrado son su tensión y su intensidad; la del circuito
eléctrico, en relación con la corriente que circula, es su
resistencia.
Estos tres factores están
íntimamente relacionados entre sí, de modo tal que alterando
el valor de cualquiera de ellos, se modifican los valores restantes o por
lo menos uno de ellos.
En la parte izquierda de la Fig.1, se
muestra un circuito eléctrico cerrado, constituido simplemente por
una pila para linterna (P), un foquito o lamparita de linterna (R) y dos
conductores (C) que conectan los terminales de la pila con los del foquito.
A la derecha se muestra el mismo circuito en símbolos.
L3 Elec-2 - 1/15
|
|
RADIO INSTITUTO
Estas experiencias permiten deducir
que: la intensidad de la corriente que circula por un circuito cerrado
depende de la tensión que actúa sobre él y de su valor
de resistencia. Las variaciones de intensidad son directamente
proporcionales a las de tensión (una aumenta cuando aumenta la otra)
e inversamente proporcionales a las de resistencia.
Las dos cosas que podemos variar manualmente
en el circuito son: la tensión y la resistencia. Como consecuencia
se modificará automáticamente la intensidad.
No tiene sentido decir que si
modificamos la intensidad de un circuito, obtendremos como consecuencia una
modificación de la tensión o de la resistencia. Corresponde
decir que si se ha modificado la intensidad de un circuito, es porque se ha
variado la tensión que actúa sobre él o la resistencia
del circuito.
LA LEY DE OHM
Se denomina 1 voltio al valor de
tensión que debe actuar sobre un circuito de 1 ohmio para que
circule una intensidad de 1 amperio. La misma relación puede
indicarse diciendo que 1 amperio es la intensidad que circulará por
un circuito de 1 ohmio, cuando sobre él actúe una
tensión de 1 voltio.
Teniendo en cuenta que las
variaciones de intensidad son directamente proporcionales a las de
tensión e inversamente proporcionales a las de resistencia, podemos
indicar esto en símbolos de la siguiente forma:
I = V / R
(1)
Donde I es el valor de la intensidad
en amperios, V el de la tensión en voltios y R el de la resistencia
en ohmios. Esta es la expresión de la LEY DE OHM.
De la misma se deducen estas otras
dos:
V = I X R
(2)
R = V / I
(3)
APLICACIONES DE LA LEY DE OHM
 A continuación plantearemos y resolveremos
algunos ejemplos de aplicación de la ley de Ohm,
de importancia fundamental en todos los problemas de electrónica.
En la Figura 4, se muestra un
circuito constituido por una batería de 45 V y una resistencia de 10
Ω que puede ser el filamento de una lámpara, un resistor de
alambre o cualquier otro accesorio.
Deseamos conocer el valor de la
intensidad que circulará por el circuito.
Aplicando la fórmula (1)
resulta:
I = V / R = 45 / 10 = 4,5
A
En este ejemplo hemos supuesto que
el amperímetro y la batería no ofrecen resistencia.
En realidad sus valores de
resistencia deben sumarse a los que se indican en el circuito, aunque
cuando son muy pequeños no alteran el resultado final.
En el circuito de la Figura 5 el
valor de la resistencia es de 15 Ω y el de la intensidad de 0,1 A.
L3 Elec-2 - 3/15
|
|
RADIO INSTITUTO
Como se vé,
disponiendo de una batería de tensión conocida, de un microamperímetro o miliamperímetro y de
otro resistor de valor conocido, puede calcularse por las indicaciones de
intensidad del instrumento, el valor de un resistor desconocido que se
conecta en serie con el circuito. Este es el principio de funcionamiento de
los óhmetros que se emplean con más
frecuencia en electrónica.
En la práctica los valores de
resistencia se escriben directamente sobre la escala del instrumento, pues
todos los demás valores son conocidos y constantes, con
excepción de las resistencias que se miden y de las intensidades que
les corresponden.
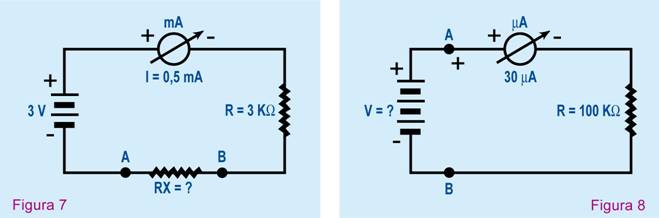
En la figura 8, se muestra un
circuito constituido por un microamperímetro,
un resistor R de 100 kΩ y una batería
cuya tensión se desea conocer, sabiendo que el microamperímetro
marca una intensidad de 30 μA (0,00003 A). Aplicando
la fórmula 2 tenemos:
V = I X R = 0,00003 X 100.000 = 3V.
Si al conectar otra batería
diferente a los terminales A y B, el instrumento marca 40 μA, el valor de tensión de esa batería
será;
V = 0,00004 X 100.000 = 4V.
Este es el principio fundamental de
los voltímetros. La batería o los dos puntos del circuito
cuya diferencia de potencial se desea medir, se conecta a los bornes o
terminales A y B. Las tensiones correspondientes se marcan directamente
sobre el instrumento, ya que el valor de R es conocido en cada caso.
Si el valor de resistencia interna
del microamperímetro es relativamente
alto, respecto del de R, se lo debe considerar restándolo del valor
calculado para todo el circuito.
SENSIBILIDAD DE LOS VOLTÍMETROS
Cuando se emplea un
miliamperímetro con escala total de 1 mA
para realizar un voltímetro, el cálculo indica que
deberá emplearse un valor total de resistencia en el circuito, a
razón de 1.000 Ω por cada voltio. Para que la aguja del
instrumento marque 100 V al final de la escala, deberá intercalarse
un resistor R de 100.000 Ω
Por esa razón se dice que la
sensibilidad de este voltímetro es de 1.000 ohmios por voltio.
Los voltímetros más
convenientes para todos los trabajos de electrónica, deben tener una
sensibilidad de 20 kΩ / V o mayor, para que
al ser aplicados a dos puntos de un circuito entre los cuales desea medirse
la diferencia de potencial, no se altere en forma importante las
características del circuito (valor de resistencia entre los puntos
a medir), lo cual alterará la tensión que realmente
había entre esos puntos, antes de conectar el voltímetro.
L3 Elec-2 - 5/15
|
|
RADIO INSTITUTO
Las intensidades I2 e I3 resultan
de:
I2 = 6 / 60 = 0,1 A
I3 = 6 / 20 = 0,3 A
La suma de las tres corrientes
derivadas resulta ser efectivamente de 0,6 A
Los valores de las corrientes
derivadas son inversamente proporcionales a los valores de resistencia de
las ramas por las cuales circulan. A través de R3 circula una
intensidad tres veces mayor que a través de R2, porque R3 es
tres veces menor que R2.
La segunda ley de Kirchhoff dice que: la suma algebraica de las
caídas de potencial (positivas) y de las f.e.m. (negativas) de un circuito cerrado, es igual a
cero.
PUNTOS EQUIPOTENCIALES
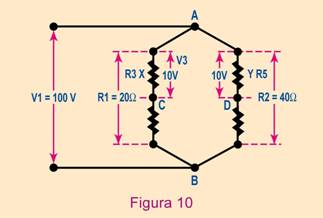 En la Figura 10, se muestra un circuito
constituido por dos resistores: R1 y R2, conectados en paralelo entre
sí y con sus extremos conectados a los terminales de una
batería de 100V.
Sobre el resistor R1, de 20 Ω,
debe haber un punto C que tenga una diferencia de potencial de 10 V con
respecto al punto A. Entre el punto A y el punto C el valor de resistencia
R3 que debe haber, puede calcularse por medio de la fórmula:
R1 X V3
R3 = ------------------
(4)
V1
Con los valores del circuito, el valor de R3
resulta:
20 X 10
R3 = -------------- = 2 Ω
100
Sobre el resistor R2, de 40 Ω,
existe también un punto D que está a una diferencia de
potencial de 10 V respecto de A. Entre esos dos puntos, el valor de
resistencia R5, calculado por la misma fórmula (4), pero
considerando a R2 en lugar de R1, es:
40
X 10
R5 = ----------------- = 4 Ω
100
Los puntos C y D que están a igual
potencial respecto del punto A (10V) y también a igual
potencial respecto del punto B
(90V), se denominan equipotenciales, es decir que no tienen
diferencia de potencial entre sí.
Cualquier punto que se considere sobre el resistor
R1 tendrá un punto equipotencial sobre el resistor R2.
Al conectar entre sí dos puntos
equipotenciales:
1) no circula corriente por el conductor que los
une y
2) el circuito al que pertenecen no se altera
con respecto al valor óhmico total y por lo tanto con respecto a la
intensidad total circulante.
L3 Elec-2 - 7/15
|
|
RADIO INSTITUTO
EL PUENTE DE WHEATSTONE (se pronuncia uiston)
Al unir entre sí dos puntos
C y D de circuitos como los de las Figuras 10 y 11, por medio de un microamperímetro, su aguja nos indicará
si los referidos puntos son o no equipotenciales.
En la Figura 12 se indica esta
disposición y en el momento en que el microamperímetro
muestra que los puntos C y D son equipotenciales, se comprueba que entre R1
y R3 existe la misma relación de valores que entre R2 y Rx, lo cual se expresa así:
R1
R2
---------- = ---------
R3
Rx
De donde se deduce que:
R2
X R3
Rx = -----------------------
(5)
R1
Esta fórmula indica que, en
un circuito como el de la Figura 12, denominado circuito en puente,
cuando el microamperímetro indica que no
circula corriente entre los puntos C y D, puede calcularse el valor de una
de las cuatro resistencias, cuando se
conocen los valores de las otras tres, sin necesidad de considerar
el valor de la tensión que actúa sobre el circuito.
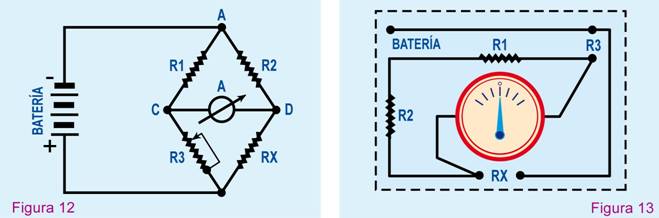
Si en el caso de la Figura 12 los valores de
resistencia fueran: R1 = 30
Ω; R2 = 50 Ω; y R3 = 70 Ω, en el momento en que C y D son
equipotenciales el valor de Rx es:
50 x 70
R x = ------------------ = 116,67 Ω
30
Cuando entre los puntos C y D
existe una diferencia de potencial, se dice que el puente está en
desequilibrio y no es aplicable la fórmula (5).
La disposición indicada en
la Figura 12, se conoce con el nombre de Puente de Wheatstone
y sirve para medir valores de resistencia con muy alta precisión y
exactitud.
Hay varias formas diferentes de
disponer los resistores en el puente de Wheatstone.
Una de ellas consiste en utilizar valores iguales entre sí para R1 y
R2, con lo que Rx resulta de igual valor que R3, cuando
el puente está en equilibrio.
Este equilibrio se obtiene variando
el valor de R3 hasta conseguir que el microamperímetro
indique cero.
Aumentando el valor de R3, la aguja
del instrumento se desviará en un sentido y disminuyéndolo
desviará en sentido contrario. Por eso conviene que la aguja del
instrumento marque el cero en el centro de la escala. En la Figura 13, se
muestra una disposición práctica de los accesorios en esta
forma de puente de Wheatstone.
L3 Elec-2 - 9/15
|
|
RADIO INSTITUTO
2) Para obtener un valor de
resistencia dado, se ubica un terminal en la
ficha hacia el lado A del primer resistor que exceda al valor deseado. El
otro terminal se conecta a la ficha A, si el
valor es impar, o a otra ficha que se determinará, si es par.
3) Debe anularse cualquier resistor
que sumado al primero, o a los que se sigan tomando, exceda del valor
deseado.
Con este sistema es posible llegar a
obtener todos los valores de resistencia entre 1 y 1.048.575 Ω
utilizando solamente 20 resistores, mientras que con el sistema de la caja
en décadas deben utilizarse 54 resistores para llegar a 999.999
Ω, en ambos casos con diferencias de 1 Ω entre dos valores consecutivos.
OTRAS
FORMAS DE PUENTE DE WHEATSTONE
Otra forma práctica de puente
de Wheatstone es la que se muestra en la
Figura16, en la que el resistor R1, que se intercala en el circuito, se
elige por medio de una llave selectora. Cuando R1 tiene igual valor que R2,
entonces Rx tiene el mismo valor que R3, por lo
cual sobre este punto de la llave selectora se marca x1.
Si se conecta R1 con un valor 10
veces menor que R2, entonces los valores de Rx
serán 10 veces mayores que los de R3, cuando el puente está
en equilibrio. En este punto de la llave selectora se marca x10. Tomando
para R1 un valor 100 veces menor que R2, el punto correspondiente de la
llave se marca x100 etc.
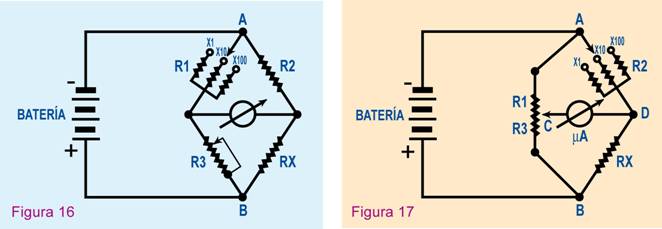
Este sistema es uno de los
más empleados en la práctica. Otra disposición
interesante de los accesorios es la que se muestra en la Figura17, donde R1
y R3 son las dos partes de un potenciómetro y el punto C del puente
es el brazo móvil de éste.
Entre A y D se conectan valores de
resistencia que son generalmente de 1, 10, 100, etc
Ω. La escala del potenciómetro se marca con números que
corresponde a la relación que hay entre los valores de resistencia
de la porción C-B y la porción C-A, para cada posición
del potenciómetro. Al usar el aparato, cuando el puente está
en equilibrio el valor medio es igual a lo que marca el dial, multiplicado
por la indicación de la llave selectora.
El mismo principio de
operación del puente de Wheatstone, se
aplica, con pequeñas variantes, a la medición de otros
accesorios empleados en electrónica (inductores, capacitores,
impedancias, etc.)
Estos conjuntos se conocen, en
general, con el nombre de puentes de impedancia o también
puentes L-C-R.
L3 Elec-2 - 11/15
|
|
RADIO INSTITUTO
En cualquier circuito puede
reemplazarse a tres resistencias conectadas entre sí en
triángulo por tres conectadas en estrella equivalente o viceversa,
sin que se alteren las características eléctricas del mismo.
A la izquierda de la Figura 20,
hemos vuelto a dibujar el circuito de la Figura18, considerando al resistor
R5 de 5 Ω, como formado por dos resistores R23 de 10 Ω cada uno,
en paralelo entre sí. Tenemos así formados dos
triángulos: 1-2-3 y 2-3-4, cada uno de los cuales puede ser
reemplazado por su circuito estrella equivalente, como se ve a la derecha
de la Figura 20.
 Este circuito se resuelve en su valor total con
facilidad, pues el valor A-2 se encuentra en serie con el 2-B y el A-3 en
serie con el 3-B, quedando los dos valores resultantes en paralelo entre
sí.
Una vez calculado el valor de
resistencia total del conjunto, será fácil calcular la
intensidad total que circula para cualquier valor de tensión que se
considere aplicado a los puntos 1 y 4.
Este valor de intensidad permite
calcular las caídas de potencial que se producen en la Figura 20
entre 1-A, entre A-B y entre B-4. Conocida la tensión entre A-B se
calculan las intensidades que pasan por A-2-B y por A-3-B, para obtener
finalmente la tensión que hay sobre el punto 2 y sobre el punto 3,
que corresponden con los marcados C y D en la Figura 18.
La diferencia de potencial que
existe entre esos dos puntos, dividida por la resistencia que hay entre
ellos, nos da la intensidad que circulará por el resistor de 5
Ω, que representa al microamperímetro
del puente de Wheatstone.
SHUNTS
En los diversos aparatos
electrónicos deben medirse intensidades tan bajas como unos pocos
microamperios y tan altas como varios amperios.
Este amplio rango de valores puede
medirse con un solo instrumento de medición, conectándole en
paralelo resistores de valores apropiados, a los cuales se los denomina
vulgarmente shunts, palabra inglesa que
puede ser reemplazada, en este caso, por la denominación de
resistores en derivación o en paralelo.
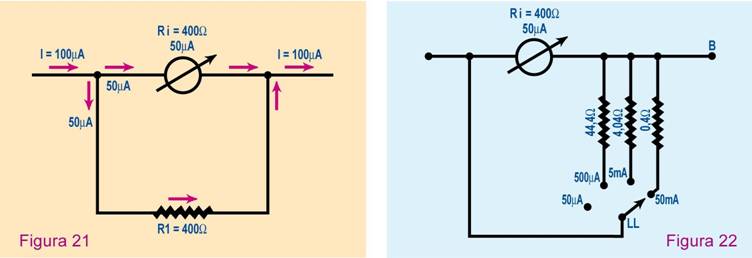
En la Figura 21, consideramos a un
instrumento con escala máxima de 50 μA
y una resistencia interna de 400 Ω, el cual está intercalado en
un circuito por el cual circula una intensidad de 100 μA.
Conectando un resistor de 400 Ω
en paralelo con el instrumento, la corriente de 100 μA
encontrará dos caminos de igual resistencia y se dividirá en
dos partes iguales de 50 μA cada una.
L3 Elec-2 - 13/15
|
|
RADIO INSTITUTO
Esto se evita con el montaje que
muestra la Figura 23. La escala de menor intensidad que se obtiene es
siempre algo mayor que la intensidad original del instrumento empleado.
El valor total que forman los resistores R1, R2,
R3 y R4 se calcula considerando el valor de resistencia interna del instrumento y la
ampliación que resulta de considerar la menor escala deseada y la
que indica originalmente el instrumento. Si la escala deseada es de 50 μA y se emplea un instrumento de 40 μA con 500 Ω de Ri,
estos cuatro resistores deben sumar:
500
R
= -------------------- = 2.000 Ω
1,25-1
El valor de 1,25 es la
relación que existe entre 50 y 40 μA.
Si el segundo rango debe ser de 500 μA, la
ampliación que se obtiene desde el instrumento de 40 μA es de 12,5 veces.
La fórmula que se aplica para calcular el
valor del resistor R4 es:
Rx
(A-1) – Ri
R4
= -----------------------
(9)
A
Si el segundo rango debe ser de 500 μA, la ampliación que se obtiene desde la
escala del instrumento es de 12,5 veces y el valor de R4 resulta:
(2.000 X 11,5) - 500
R4 = ------------------------------------- = 1.800 Ω
12,5
Si los rangos subsiguientes son de
5.000 μA (5 mA) y
de 50 mA, los resistores R3 y R2 son 10 y 100
veces menores, respectivamente, que R4. El valor de R1 es lo que falta para
completar el valor calculado de 2.000 Ω.
RESISTENCIA INTERNA DEL MILIAMPERÍMETRO
 Para calcular el valor de los shunts
es necesario conocer el valor de Ri del
instrumento empleado y pocas veces los instrumentos llevan marcado este
valor. Para medirlo (Figura24) basta medir un valor de intensidad cercano
al mayor valor original del instrumento, anotando ese valor. Luego se
conecta un shunt cuyo valor de resistencia R sea
lo más exacto posible. Se anota el nuevo valor de intensidad que
marca el instrumento.
El resultado de dividir las dos
indicaciones es la ampliación A obtenida. El valor de Ri del instrumento se obtiene por la siguiente
fórmula:
R i = R X (A - 1)
(10)
Si suponemos que en una primera
medición de intensidad del instrumento indicó 45 μA y al conectarle en paralelo un shunt de 400 Ω marcó 20 μA
la ampliación A resultó de 2,25 veces, por lo que el valor de
Ri del instrumento es:
R i = 400 X (2,25 - 1) =
500Ω
El error será tanto menor cuanto más alta es la resistencia de todo el
circuito, en relación al valor del shunt
que se emplea. Una relación aceptable es de 50 ó cualquier
valor mayor.
En el caso de la Figura 24, la
relación es de 170. (68.000 / 400 = 170)
RADIO
INSTITUTO
L3 Elec-2 - 15/15
|
|
|
R A D I O I N S
T I T U T O
MATRÍCULA
----------------------- NOMBRE Y APELLIDO
------------------------------------------------------------------
CALIFICACIÓN
----------------------------------- CALLE ---------------------------------------------------
Nº ----------------
FECHA DE ENVÍO
--------------------------CÓDIGO ----------------- LOCALIDAD
---------------------------------------
PAÍS
---------------------------------------------
CURSO DE ELECTRÓNICA
- 2
EXAMEN DE LA LECCIÓN Nº
3
1) En un
circuito como el de la Figura 2, al aumentar la tensión, la
intensidad:
A = aumenta;
B = no varía,
C = disminuye.
2) En un
circuito como el de la Figura 2, al aumentar la resistencia, la
intensidad: A = aumenta; B = no varía, C = disminuye.
3) Un
circuito eléctrico cerrado está formado por una
batería de 9 V y un resistor de 22 kΩ:
La intensidad circulante es de: A = 0,41 mA;
B = 2,44 mA;
C = 198 mA.
4) Un
circuito eléctrico cerrado está formado por una
batería, un resistor de 43 kΩ y por
el mismo circula una intensidad de 1 mA. La
tensión de la batería es: A = 1,5 V;
B = 9V;
C = 43 V.
5) En un
puente de Wheatstone, como el de la Figura 12,
el resistor R3 tiene 350 Ω, R2 tiene 1.000 Ω y R1 tiene100
Ω. Cuando el puente está en equilibrio (el instrumento marca
0) el resistor Rx que se mide tiene:
A = 4.260 Ω;
B = 3.500 Ω;
C = 1.000 Ω
6) Los
efectos que producen las corrientes eléctricas y que se aprovechan
en los instrumentos de medición, son: A = magnéticos;
B = luminosos;
C = mecánicos.
7)
Disponemos de un microamperímetro de 50 μA y deseamos formar con él un
voltímetro con escala 0-1.000 V. El resistor que debemos
conectarle en serie es de:
A = 200 kΩ; B = 2 MΩ; C = 20 MΩ.
8) En un
circuito como el de la Figura 21, hemos conseguido que la aguja del
miliamperímetro descienda exactamente a la mitad de la escala
cuando se le conecta en paralelo un resistor de 300 Ω. El valor de Ri del instrumento es: A = 150 Ω;
B = 300 Ω;
C = 45.000 Ω.
9)
Tenemos un miliamperímetro de 10 mA.
Cual es el límite máximo de corriente que puede medirse con
él de modo directo, es decir, sin shunt: A = 10 mA B =
100 mA
C = 1.000 mA
10)
Disponemos de tres voltímetros con sensibilidades de 1.000 Ω
X volt; de 20.000 Ω X volt
y de 50.000 Ω X volt. Cual es el
más sensible?: A = el de 1.000 Ω X volt B =
El de 20.000 Ω X volt C = El de 50.000
Ω X volt.
|
* RESPUESTAS AL EXAMEN DE LA LECCIÓN Nº
3 *
|
|
PREGUNTAS
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
A
|
|
|
|
|
|
|
|
|
|
|
|
B
|
|
|
|
|
|
|
|
|
|
|
|
C
|
|
|
|
|
|
|
|
|
|
|
Marque con una cruz la casilla que corresponde a la
contestación correcta
NUNCA marque 2 cruces en una misma columna.
|
Esta imagen del examen
está en formato Word para que pueda confeccionarlo fácilmente
en la computadora. Bájelo a la PC, ponga las cruces en los
casilleros de las respuestas, según su criterio, mediante el
programa de Word, y luego lo envía por mail a la escuela. Se lo
devolveremos calificado, con sello y firma de RADIO INSTITUTO. Si la nota
es 10, irá acompañado de la lección 3 completa. Si es
un puntaje menor, usted decide si la quiere recibir o no de acuerdo a los
descuentos vigentes (vea la nota).
Para bajar la imagen del examen,
lo mejor es copiarla y pegarla en una página de Word. Si algo sale
deformado o corrido, intente arreglarlo con el programa o déjelo
así si no molesta mucho. Como no tenemos ficha con sus datos de
alumno, ponga solo nombre y apellido, localidad y país; nosotros
completaremos la Nota.
|
IR A LECCIÓN 26
VOLVER A
RADIO INSTITUTO - INDEX
|
